Abstraction and the Bayesian Occam's razor

Abstraction is a fundamental aspect of programming. It's a tool that often relies on a lot of human intuition, not always on clear principles.

Programming can be thought of as modeling domains and the solutions to problems. Models are subject to overfitting and underfitting. This means that good abstraction is often about finding that sweet spot in between.

There are conflicting concerns when choosing abstractions: They can enable reuse, which is usually a good thing. They often reduce the number of lines of code you have to write. However, abstractions can also increase coupling which can cause other problems. Once a component is widely used, modifying it to fit a new use case risks breaking the existing use cases. There are trade-offs.

For example, to use the standard metaphors, maybe the problem to solve involves something that looks like a dog, so you write a Dog component. Then you encounter a cat so you're about to write a Cat component but wait! You notice they share a lot of characteristics so you refactor the previous component into an Animal component that can handle both through configuration.

Later on, you encounter a problem that looks like a lizard, another animal. Easy! Just reuse the Animal component.

But then, when you start modifying Animal’s code to support lizards you find out cats and dogs have hair, lizards have scales, cats and dogs have warm blood, but lizards are cold blooded. It's hard to modify Animal to fit the lizard case without breaking cats and dogs. This could be a sign that you should have abstracted to Mammal, not Animal and kept Lizard separate (they might still share some interfaces though).

How do you make these decisions? It's not easy, a very old problem. In practice, the solution unfortunately is usually just using intuition and common sense. But this doesn't mean that there doesn't exist more principled ways to think about this and it can help to build that intuition to know about them.

You can think about abstraction using the concept of Bayesian Occam's Razor.

Let's start with an example. Here is a tree and some boxes (from the link above):

Should you model this scene as having a single box hidden behind a tree or two boxes? Think of it in terms of writing a program that draws that landscape and deciding whether to use one function per side of the tree or one that draws both sides as a single rectangle (generative programs are a good way to think about reasoning and models in general).

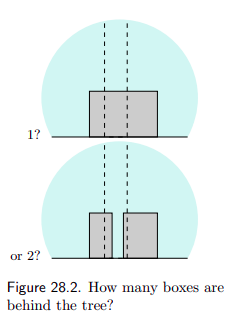
A similar decision has to be made when choosing abstractions. Should you pick the abstraction that allows you to write less code while covering more area? Which choice is going to be more maintainable and durable?

If you read the book chapter, it lays out calculations that assign probabilities to both scenarios so that you would know how often you'd be right picking one or the other (given priors, assumptions about how large boxes tend to be etc.).

Spoiler: the single box is more probable with this problem. However, one thing to notice in the math, is that there are terms that appear in the equations that depend on the resolution of the image and the width of the tree.

This is because the choice of the optimal model depends on the uncertainty you have about the reality behind the data, about what you know and don't know about the domain.

For example, if we were able to zoom in on the image of the tree, we might see that the edge on one side of the tree is a tiny bit higher than the edge on the other side of the tree. This would give much more weight to there being two boxes. If you wished to keep the single object abstraction, you might have to turn it into a more complex shape with two top levels (but note that the code for that might be longer and harder to test than using two simple boxes).

Alternatively, if we zoomed in and the lines remained equal, this would give more weight to there being only one box, more weight than before zooming in. The extra resolution would increase certainty. The area of the box(es) hidden by the tree also affects the results of the calculation. If the tree was really thin, it would be less likely that there were two boxes that just happened to both end in the tiny hidden area.

A large trunk increases the probability of two boxes. There's more ways that two boxes can fit behind a large trunk.

The more domain knowledge you have, the more clarity, the more resolution, the better you are able to choose the right abstraction.

I'm using statistical models as a metaphor for code. You might think this is stretching the metaphor.

However, if you click on the link, the last section before the conclusion is titled "Minimum Description Length" (MDL). This article is written by a mathematician that advocates doing the math to get answers, but it acknowledges that it’s been shown that this is equivalent to selecting the shortest program that can generate the relevant data.

One important thing to note about MDL, is that it's not just about creating the shortest program that gives you an answer, it's the shortest program that can generate your dataset of questions and answers (the knowledge used to create the model).

That knowledge might not be available in code but a proxy for this might be the set of automated tests you would have to write to describe all the known use cases.

According to MDL, you must include the size of the tests in what you are trying to minimize. Some abstractions will allow you to write fewer tests and still be confident in your code, it will make some tests redundant or easier to combine into iterative tests.

It's important to be honest with yourself here, just cutting out the tests, or removing other safeties like strict types doesn't give you a lower MDL, in that case, you're missing the descriptions of important parts of your data or knowledge. Even if you don't intend to have full test coverage, you have to think in terms of potential tests when reasoning about reducing code size. How much smaller would your hypothetical full test coverage be given your choice of abstraction.

Note that there is also a distinction between code that adds to the state space, like new logic dealing with new use cases, and code that reduces state, like tests and strict types. These are opposite in some fundamental ways. Unlike use case logic, adding test code doesn't cause you to need even more tests to get confidence.

Code that isn't necessary for the computation, that's there solely to clarify things for humans shouldn't be counted. For example, descriptive variable names and comments have benefits and don't count towards MDL size. Think about the minified version of the code for MDL purposes.

Reducing MDL of logic and potential tests, improves the fit between abstractions and use cases, between problem and solution (this type of reasoning even extends to product/market fit).

It doesn't just allow you to have less code to maintain (that's just a bonus). Reducing overfitting or underfitting, actually makes your model more predictive and more correct in more future unknown cases. It reduces the chances of things breaking when facing new situations, when facing interpolations or extrapolations of known situations. MDL and the Bayesian Occam's Razor are designed to optimize for generalization into the unknown.

There is an incredible kind of "divine coincidence" happening here. Playing a bit of code golf doesn't only give you less code to maintain in the future (and often more computing efficiency), but it also makes your code more correct in the face of uncertainty. It means you are less likely to have to refactor the abstraction in the future.

This explains why lines-of-code measures of developer productivity are so despised. A lot of developers have the correct intuition that increasing code length goes directly against a good fit between problem and solution.

I hope this provides some insight into how to choose abstractions, that there actually exists a solution between too much and too little abstraction and principles to find it. Unfortunately the optimal solution is often hard to find. The smallest MDL code you can theoretically write to model a problem and its data is called its Kolmogov Complexity. This theoretical limit is uncomputable.

Acknowledgements: Thanks to Grant Oladipo and other engineers at Pulley (YC W20) for discussions that led to this post.