The unreasonable effectiveness of failure
Science works by trial and error. You make a theory, you then test that theory with data. You can argue all of human progress works this way, including technology creation, business innovation etc. However, the error part of trial and error is often underappreciated.
Processes or regulations that try to reduce the risk of failures too much also necessarily inhibit progress.
Here's the mathematical argument.
You can think of iterative improvement processes as monte carlo algorithms (for a clue of the shape of these algorithms, the term monte carlo indeed comes from the casino). These seem to work best when attempts, when iterations are somewhat random in size, are distributed in a bell curve around the current state. Markov Chain Monte Carlo Metropolis Hastings (MCMH) algorithms are designed to explore an irregular complex space without getting stuck in local optima.
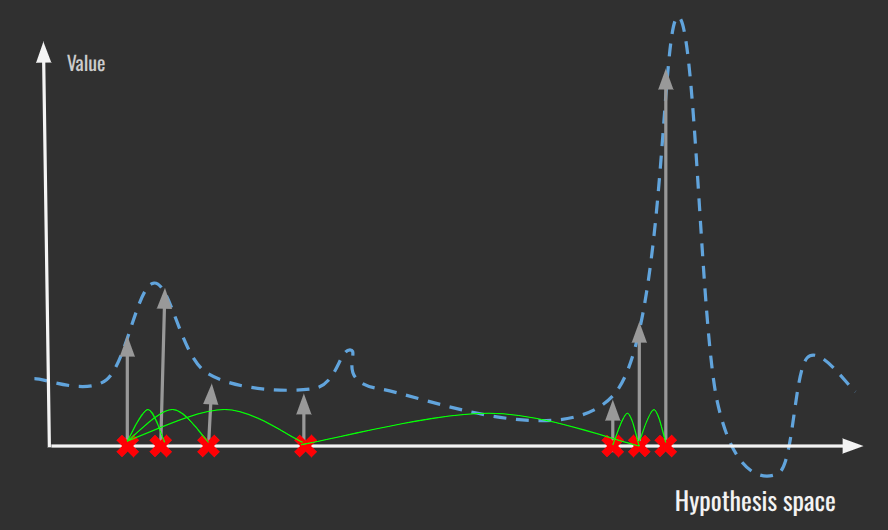
At a high level, these algorithms work by:
1. Jumping to a new proposed point in the state space, jumping a particular distance from the current state.
2. Measuring the effect of that change, and based on an equation, deciding whether to accept or reject the change before the next iteration (that equation is the essence of MCMH, it accepts all improvements and sometimes accepts a number of detrimental changes as well, since they could be a path to a higher global maximum).
MCMH is basically a mathematical formalization of scientific iterative trial and error.
There's a corollary. Even though these algorithms usually make the jump distribution a bell curve, with the smaller jumps for productive hill climbing and the longer tail jumps to avoid getting stuck locally, there is still the question of what the average size of iterations should be.
It turns out that there is a mathematical answer to this question. Smaller jumps tend to result in a high acceptance rate and more predictability while larger, riskier, bolder jumps tend to result in iterations that get rejected because they often land in valleys away from the hill that had previously been climbed.
It's possible to target a specific acceptance rate by varying the average size of the jumps. When the jumps tend to be rejected too often, do smaller jumps. When the jumps tend to get accepted too often, do larger jumps (this is called Adaptive MCMH).
Andrew Gelman, a Bayesian mathematician, calculated in his famous "23.4" paper that the optimal acceptance rate to target to explore a space efficiently is between 23.4% (for a two dimensional problem to 50% for a high dimensional problem).
This, in my mind, is sorta mathematically in line with the intuition for the need to try a lot of things and reject many iterations to efficiently find optimal solutions.
Now I don't think the Gelman 50% rejection target is correct for all types of iterations. The MCMH process is for algorithms where each iteration has a very low cost. For real world projects, a lot of your iterations and rejections can happen just in the thinking and planning phases. Lots of the rejected iterations can just be thought experiments. The costlier iterations when you actually build something should have a higher acceptance rate.
But thought experiments and iterations that are not actually built, are imperfect, they often don't represent the real world very well so you have no choice but to build some of the iterations (thought experiments also require a ton of domain expertise that you gain through real world experimentation).
I don't have an answer to what the correct acceptance rate should be for actually built iterations, but it's not zero.
There are striking examples out there of processes with expensive iterations with still considerable rejection rates. Elon Musk, for example, blows up a lot of rockets, an extremely expensive thing to do. Some people would say these are mistakes but the way I see it, it's a sign of a process with a tuned acceptance/rejection rate that recognizes that rejected attempts are important for the process to converge to the optimal design as fast as possible.
Not blowing up those rockets might mean evolving the design slower or even the design getting stuck in a local, insufficiently good solution.
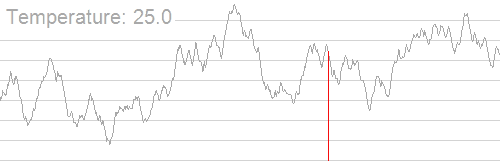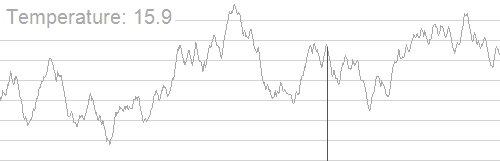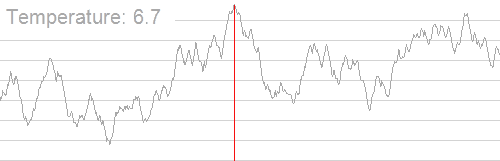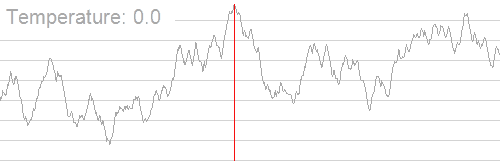
Another example of an algorithm that leverages calibrated randomness and risk, is LLMs making use of injected randomness via their temperature parameter. An LLM that always picks the next most predictable token often settles on a less optimal final output. If you play with those LLMs where you can still manually set temperature, a too low temperature gets you decidedly uninteresting, undifferentiated outputs that kind-of lose their magic.
That is, while a low temperature LLM gives you the highest probability and most predictable sentence, using a higher temperature LLM, where after generating each token, a bit of randomness is injected into the process to generate next token and each later tokens are re-evaluated according to the previously slightly randomized tokens, results in better overall output.
This is not surprising to me since the LLM neural nets are a kind of fast approximation of markov chain approaches and benefit from the same injection of risk and randomness to help get you out of local optima.
You can improve processes for innovation by ensuring that trying, failing and retrying is as quick and easy as possible.
When you can measure failure rates it should not be only to ensure they are low enough but often for the opposite, to also ensure that they are high enough to target a well calibrated acceptance rate.
Randomness, boldness and rejections and pivots are what leads to eventual exceptional results. Of course you have to be careful for failures to not be the result of poor execution, they should be due to boldness and risk taking, due to pushing the frontier, but they are an important part of the process of innovation.
This works best applied recursively at all levels from small tactical narrow scope everyday moves to large strategic wide ranging endeavors. This is also similar to LLMs which model recursive grammars and randomness can occur at any level.
So calibrate risk by swinging hard enough that you get a chance at home runs even though this will also result in a lot of strikes.
Acknowledgements: I'd like to thank TJ Wason for feedback on this post.